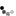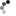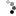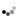Lil math puzzle

[DoesntMatter]

A staircase is created with 10 blocks and 4 steps. The goal is to relate the number of blocks, N, with the number of steps, S, for any staircase in an algebraic formula.

No handbooks/texts/google

[DoesntMatter]

Maybe this is not the kind of thing people find interesting? There are plenty of little puzzles like these I can post but if no one cares then why bother

[IndiReloaded]

I love stuff like this, but I'm not doing your homework, am I?

[DoesntMatter]

I'm in calculus II so we wouldn't be doing this. But this can be solved by applying some type of integration

[IndiReloaded]

Okay. But isn't this just calcing the sum of a basic arthmetic sequence, tho? You asked for the number of blocks.

S=1+2+3+4+5... etc.

[DoesntMatter]

No, the number of blocks in relation to the number of step or the number of steps in relation to the number of blocks

The first being easier

I gotta go finish my chem and math homework though and eat dinner with the homies I'll be back later tonight

[IndiReloaded]

No, the number of blocks in relation to the number of step or the number of steps in relation to the number of blocks

The first being easier

I gotta go finish my chem and math homework though and eat dinner with the homies I'll be back later tonight

Meaning that you want the to know how many total blocks you need to build, say, 23 steps? Or you want to know # of blocks under a *specific* step? Are you assuming the length/height of the step is a fixed postitive integer value (i.e. I can't stack blocks staggered over 1/2 a step & the block size is constant).

[lastwish]

hmmm..from what i think you are asking....i believe its:

(S-1)S + S = N
-------
2

S>1

Check if it works...haven't done calculus for a long time.

[Junket]

Oh.

My.

God.

If this is the kind of shit I have to do to get some kind of electrical engineering degree...

F*CK.

THAT.

[IndiReloaded]

hmmm..from what i think you are asking....i believe its:

(S-1)S + S = N
-------
2

S>1

Check if it works...haven't done calculus for a long time.

Ya, this this is what I was also saying (except your constant of 1/2 would just be the generic d constant for all cases), but he didn't seem to think an arithmetic series was what he wanted. And I wouldn't really call this calculus. Confused, b/c I think ^this is correct.

[Illusional]

anyone care for a beer?? i've got an extra 6 that i won't drink.

raverboy

[DoesntMatter]

Yeah lastwish solved for number of blocks in terms of S, which can be easily modified with the quadratic equation to get S in terms of N.

But the point was to show how you solved for it because there are many ways. The method using calculus is one someone else pointed out to me, not a method I would have used but works

The way I solved it was this:

N(1) = 1 when S = 1

N(2) = 3 = N(1) + 2 when S = 2

N(3) = 6 = N(2) + 3 when S = 3

N(4) = 10 = N(3) + 4 when S = 4

Which is just a summation-

_______S
N(S) = ∑ i
_______i=1
(ignore __)

Which has the closed form expression of

N(S) = 1 + 2 + 3 + …. + (S – 1) + S

Adding this to itself and dividing by 2 (taking the average)-

N(S) = 1 + 2 + … + (S – 1) + S

N(S) = S + (S – 1) + ….. + 2 + 1

2N(S) = (S + 1) + (S + 1) +…..+ (S + 1)

dividing by 2 to get N(S) = S(S + 1) / 2 since there are S terms. Luckily this expansion is well known so I didn’t need to derive it again

Lastwish what method did you use to arrive at your answer?

[IndiReloaded]

Which has the closed form expression of

N(S) = 1 + 2 + 3 + …. + (S – 1) + S

LOL, this^ is what I said DM.

Okay. But isn't this just calcing the sum of a basic arthmetic sequence, tho?

I just remembered the basic formula, tho, didn't work it out from first principles.

What was the calculus method?

[anachronistic]

A staircase is created with 10 blocks and 4 steps. The goal is to relate the number of blocks, N, with the number of steps, S, for any staircase in an algebraic formula.

No handbooks/texts/google

You suck at drawing.



No hard feelings.

[lastwish]

lol. You don't need calculus or any formula to solve this question. I used a rather primative method. I just visualized the steps as a full cube and saw that there are patterns as you increase the number of steps. This is from a humanity and social science student. Not a math and life science person.